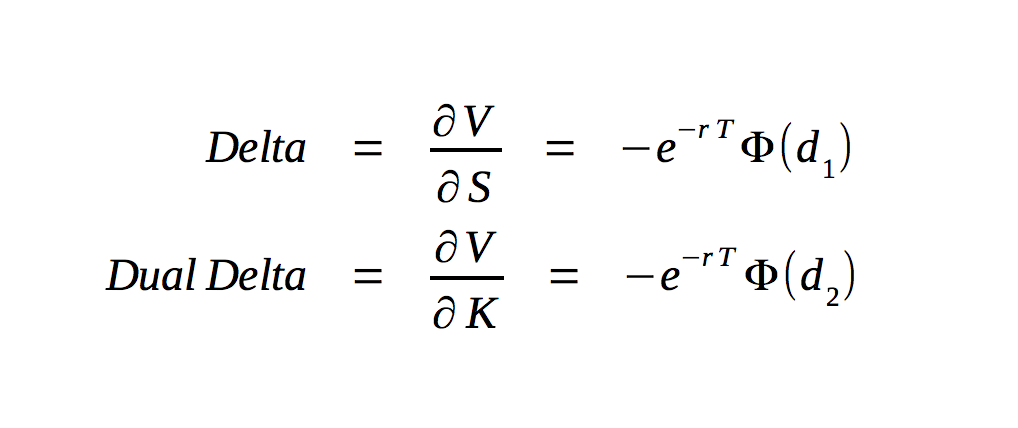Duel of the Deltas: Calculating Moneyness via Dual Delta

You would have to search long and hard to find an options trader who isn’t familiar with the concept of delta. As one of the most basic option sensitivities, or “Greeks”, delta expresses the relationship between the value of the option and the value of the underlying security. Secondarily, the delta is also sometimes used as an ad lib approximation of the percentage chance that an option will expire in the money. While this can be a quick and useful approximation, it’s not as accurate as many believe it to be. To correctly calculate the percentage chance that an option will expire in the money, one has to calculate what’s known as the “Dual Delta”.

The calculations of delta and dual delta are very similar and fairly simple. The difference results from the fact that the dual delta is the derivative of the options value with respect to the strike price, rather than the derivative of the options value with respect to the price of the underlying asset. The formula for dual delta differs from the formula for delta only in the substitution of d₂ for d₁.

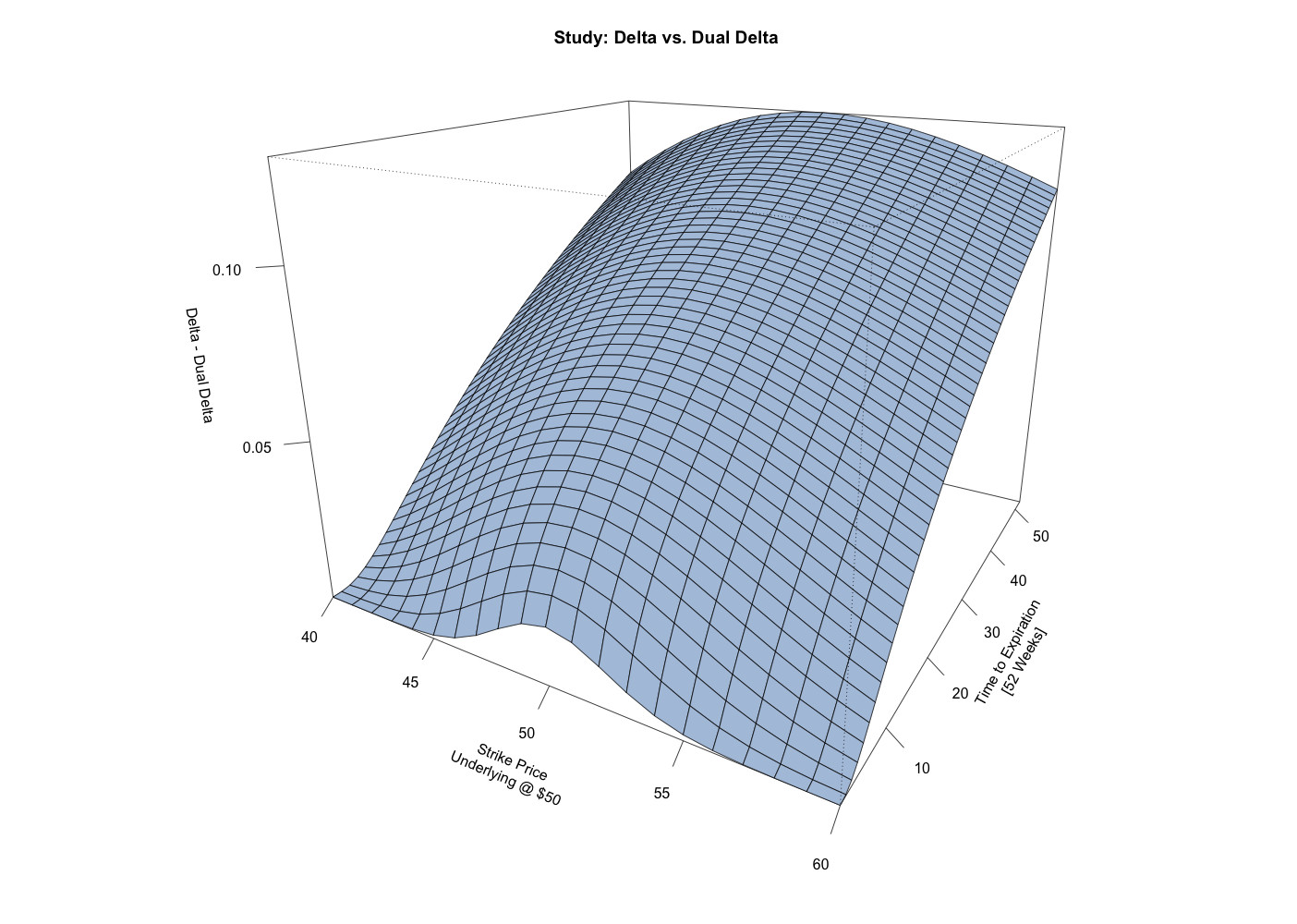
For options with a relatively short time remaining until expiration, the difference is only significant right at-the-money. However, for longer term options, especially for at-the-money options, the difference can be quite significant. For call options, dual delta is typically smaller in magnitude than delta, which implies that using call delta as a surrogate for dual delta overstates the probability of expiring in the money. For put options, it’s just the reverse. The dual delta is typically larger in magnitude than the delta, which implies that using put delta as a surrogate for dual delta understates the probability of expiring in the money.

So when formulating an options strategy that depends upon an accurate assessment of the probability of an option expiring in the money, take the time to actually calculate the dual delta. The increase in accuracy can be substantial, and might make the difference in the success of your strategy.