Volatility, Price and Delta: The Effects of Implied Volatility and Underlying Price on Delta

For options traders trying to understand how the value of an option might change given a change to one of the pricing model components, the obvious source for answers are the option sensitivities, otherwise known as the “Greeks”. What’s not as well know is that there are second-order sensitivities that can help explain how these first-order sensitivities change given a change to one of the pricing components. “Vanna” is a second-order sensitivity which describes the change in delta given a change in volatility.

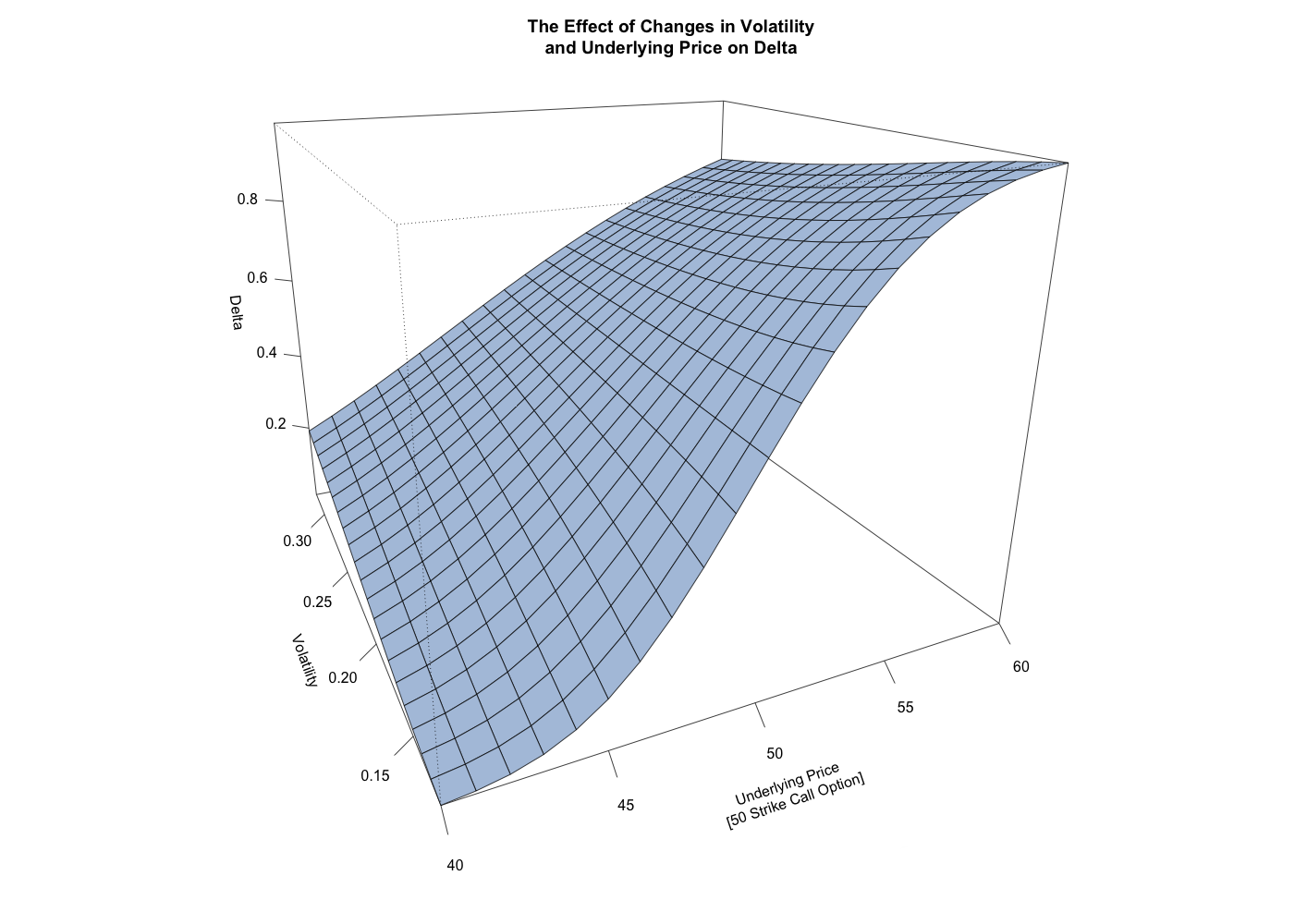
For a recent mentoring session, we were discussing the management and hedging of a complex option position, and the question came up of which volatility to use when calculating the delta for the position’s out-of-the money calls. What was initially unclear to the client was how changes in volatility might affect the delta of these out-of-the-money calls. As they say, a picture is worth a thousand words, so we put together this 3-dimensional chart, illustrating the effects of volatility and underlying price on the option’s delta.

What you’ll notice from this chart is that at higher volatilities, the range of delta across prices is much narrower and the change fairly linear. Whereas when volatility decreases, the range of delta is much wider and the change exhibits the “S” curvature that’s typical of delta, and reminiscent of the cumulative distribution function.

For our mentoring session we were concerned about the possibility of “over-hedging” these out-of-the-money calls. It was decided to use a somewhat lower volatility when calculating delta, thereby lower the delta and decreasing the hedge.